Naïve approaches

Intuition, Prior Knowledge or Expectation

How many clusters are there?

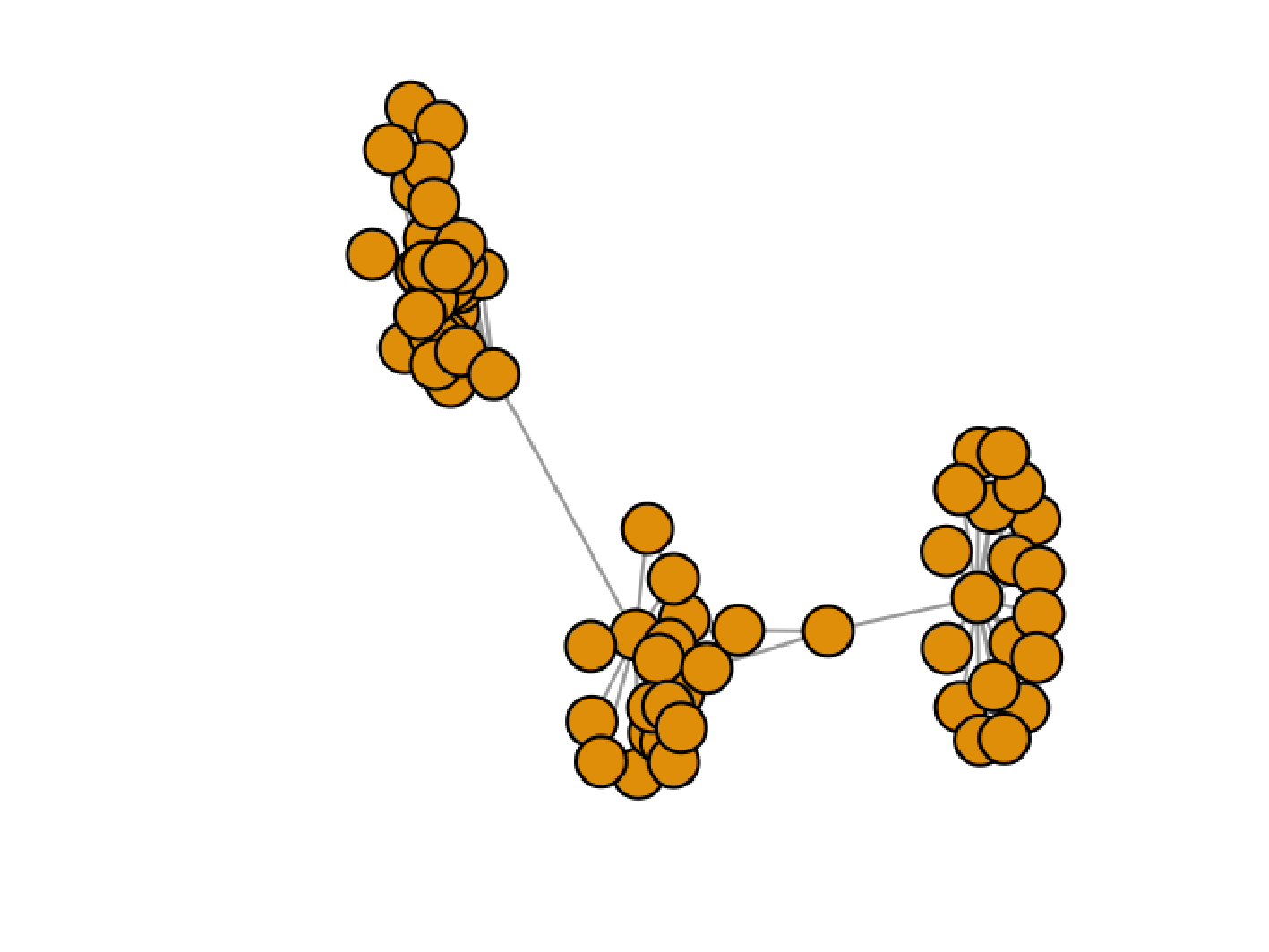
This approach is common in practice but not recommended!

Data-driven approaches

• Elbow method
• Spectral gap
• Modularity maximization

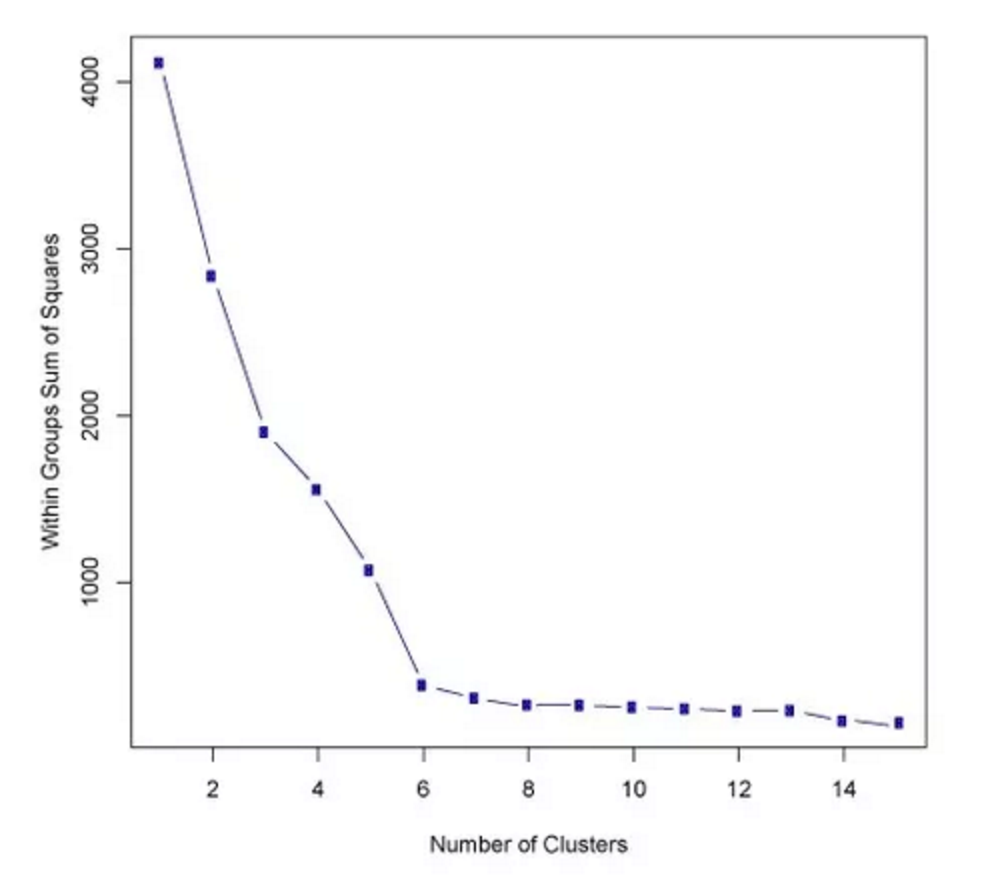
Elbow method

Intuition: find k where an additional cluster doesn't significantly add to the amount of variance explained

$$ D_k = \sum_{x_i \in C_k} \sum_{x_j \in C_k} ||x_i-x_j||^2 = 2n_k \sum_{x_i \in C_k} ||x_i-\mu_k||^2 $$ $$ W_k = \sum_{k = 1}^{k} \frac{1}{2n_k} D_k$$ $n_k$ is the number of clusters. $\mu_k$ is the mean of each cluster.

Elbow method

Daniel Martin

Spectral Gap

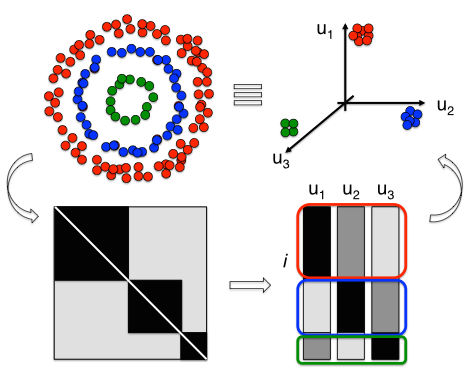
Relevant for Spectral Clustering

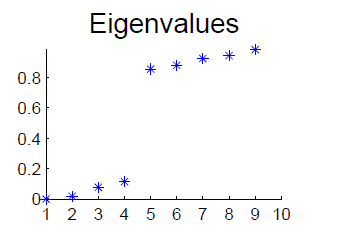
Spectral Gap

If $L$ is approximately block-diagonal, then the eigenvalue spectrum of $L$ will have a gap at the optimal k

Charles Martin

Modularity Maximization

Pratha Sah

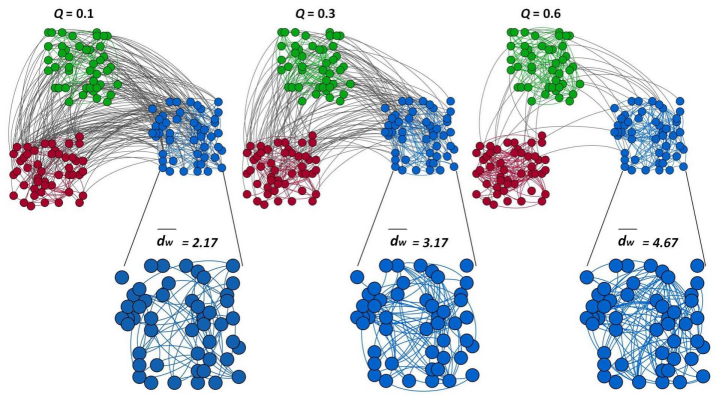
Modularity Maximization

Intuition: maximize within-cluster edges and minimize between-cluster edges

$$ Q = \frac{1}{2m} \sum_{ij} A_{ij} - \frac{k_i k_j}{2m} \delta(i, j) $$ $$ \delta(i, j) = \begin{cases} 1 & \text{if i = j} \\ 0 & \text{otherwise} \end{cases} $$

Modularity Maximization

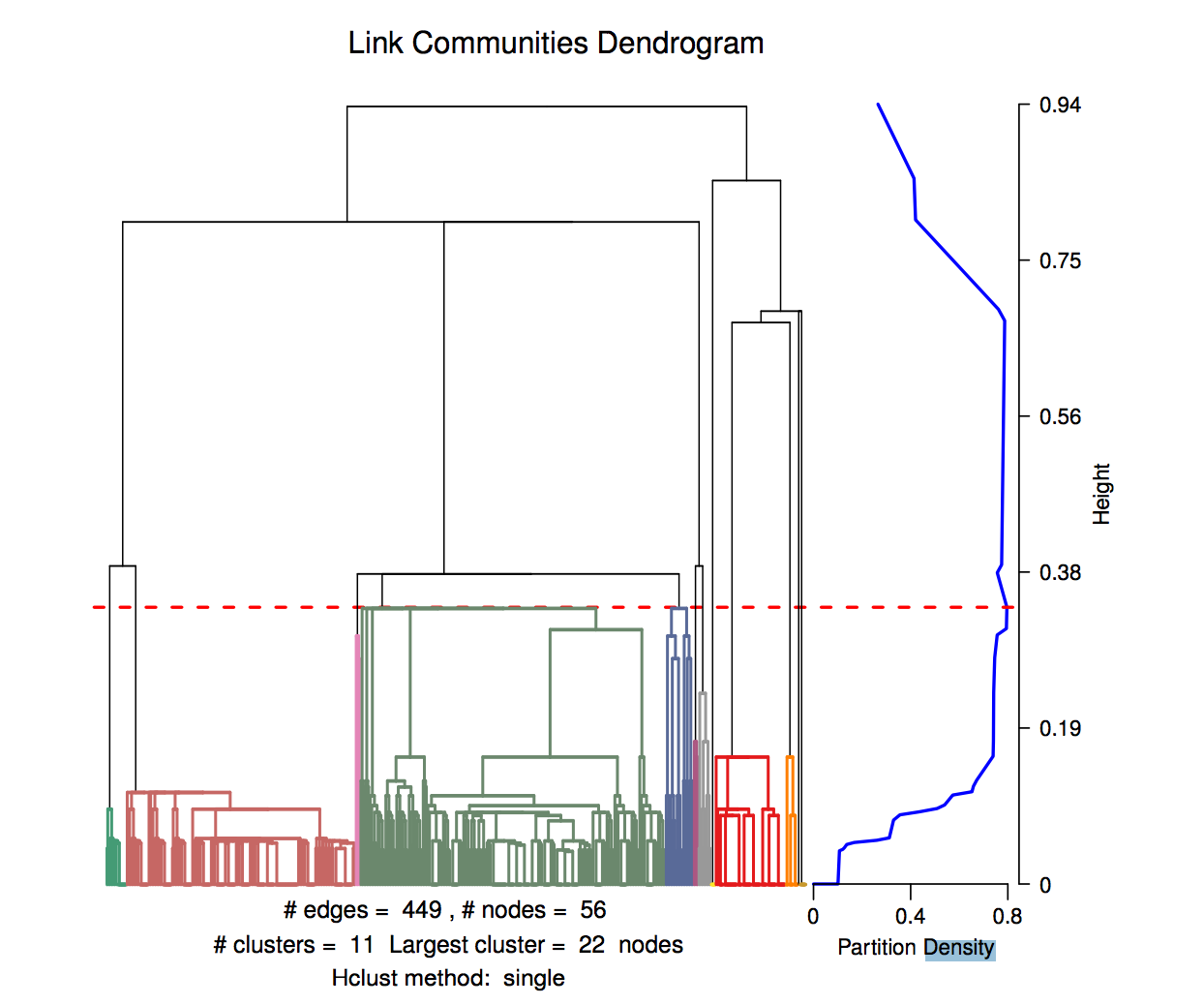
Used in Link-community clustering